Learning how to code improved how I think

The concept of emergent complexity or emergence, which any biologist or chemist will find to be intutive, can be examined in a raw form with computer science, using (among other things) cellular automata. Cellualar automata are models of computation where you take a simple set of rules and run them, which produces emergent complexity. Some cellular automata are more elaborate than others despite having a rule set of similar complexity. Want an example: how about Conway's Game of Life. Take a grid. Each square on the grid can either be live or dead. For each square in the grid, follow these rules:

1. Any live cell with fewer than two neighbors dies.
2. Any live cell with two or three neighbors lives.
3. Any live cell with more than three neighbors dies.
4. Any dead cell with three neighbors becomes a live cell.

That's it. Run it and you can get incredible patterns. If you're curious, have a look here in the Life Wiki at the various patterns that have been found. Running Conway's Game of Life is the computational equivalent of looking at a drop of pondwater under the microscope. Included in these patterns is a Turing machine, a common model for a computer used in theoretical computer science. The picture of a Turing machine below, implemented in Conway's Game of Life, is from the respective page in Life Wiki.

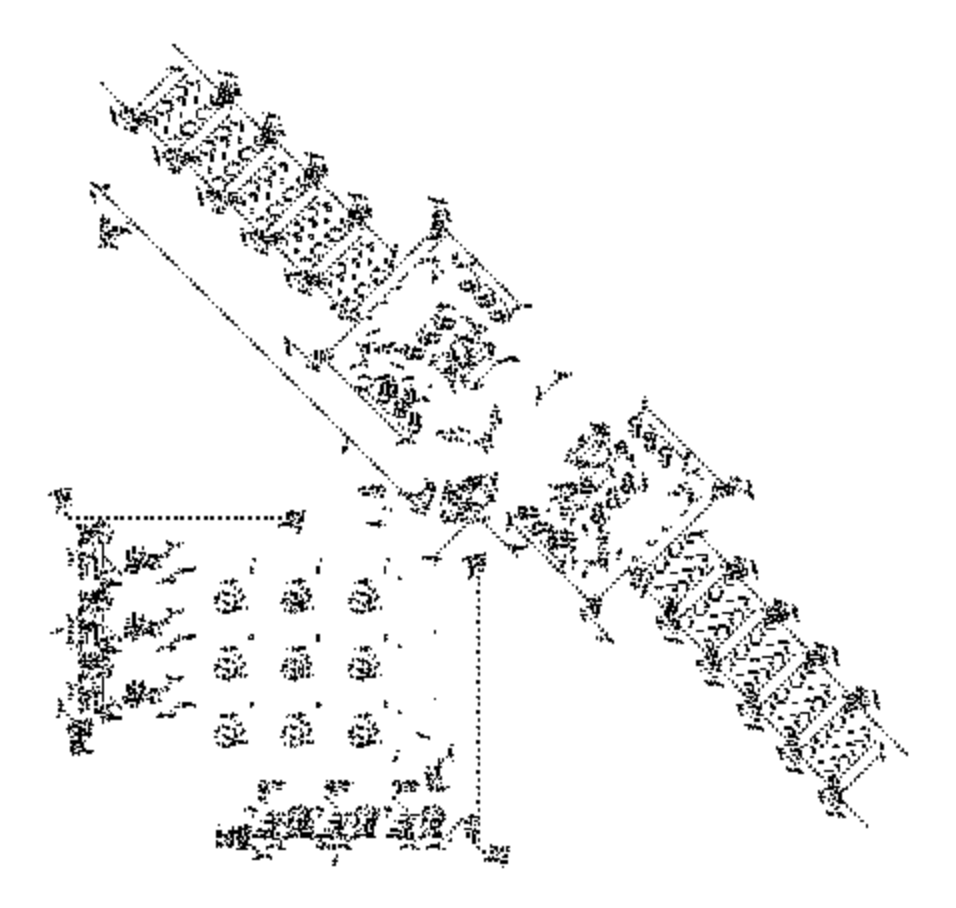
In other words, Conway's game of life is Turing complete, meaning that any form of computation that exists, from logic gates to Tetris to ChatGPT, is theoretically implementable using only Conway's game of life patterns (inefficient, but possible).

I first came across Conway's Game of Life when I was 16, there was a sort of universe-ness that was totally maxed out. It was the first time where I could conceive of our universe being made up of something like this at the very bottom. Even if it wasn't, I got the idea in my head that emergent complexity (which is perhaps the -ness that is being maxed out here) could give rise to way more than I had ever thought.

It wasn't until I was 28 and was learning how to code that I had this feeling again, and I knew I was going to pursue it for as long as I possibly could.

Email is a wonderful thing for people whose role in life is to be on top of things. But not for me; my role is to be on the bottom of things.

Donald Knuth, from Email (let's drop the hyphen)

My first computer science class was in Java. My second one was in C++. These are lower-level langugaes as compred to R and Python, the two languages that I use these days. It was through programming that I really solidified the concept of levels of analysis. We all have a general idea of what it is, like the xkcd comic here. That pschology is just applied biology is just applied chemistry is just applied physics, etc. I'll add that that by saying that as a biologist, the best biologists I know are actually chemists in disguise.

In terms of computer science, we have what are broadly called low-level languages and high-level languages. These terms are relative to your programming language of choice. If we look at the printing of "hello world" in Python for example, it looks like this:

print("hello world")

That's it. A single command. Then you run it. Then you get "hello world" on the console. But there's a ton of stuff that happens under the surface. To give you an idea of what that looks like, let's go with a lower level language. C.

#include <stdio.h>

int main() {
    printf("hello world");
    return 0;
}

So here, we need to include a library that allows us to do input/output things, which gives us the function printf. It's not just built into the language. We have to end each line with a semicolon. We have int main() which is our main function that must be called to run the thing. We're declaring the type of thing that the function returns. In this case an integer.

This brings us to the point that in C (and many other languages) you have to declare the type of object you're using. So if you have a variable x you want to set to 5, you have to say int x = 5, whereas in python you'd say x = 5. And you need a statement that the function returns. In this case 0, which by convention terminates the program. So you're also telling the computer when it terminates. It doesn't just figure it out. So there's a lot more you have to keep track of. And if you're just trying to analyze some data, it's way more convenient for the computer to sweep it under the rug.

There's a whole other piece here that I'm not going to talk about for the sake of brevity: while R and python are interactive, where you can simply type things in and they run automatically, C and other lower level languages are entirely compiled. Rather than programming interactively, you have to compile it first, or convert it into the binary machine code that will be understood by the computer's hardware. This requires the use of a compiler to turn your C file into an executable binary file, which is then read by the computer, which only then produces "hello world."

But this is just the top of the rabbit hole. If you really want to know what's going on, let's look at an even lower level language: Assembly. This is the language underneath C and everything else (save machine code). If you code in python, then C is a lower level language. If you code in assembly (which is very rare these days), then C is a higher level language. So I'm going to give you the Assembly code for printing out hello world for the ARM64 chip, which my current computer runs. This is the first point: when you're coding in Assembly, you're dealing with a different language for each chip. Now, there's a lot going on below, so if you want a better explanation from someone who actually codes in assembly, please watch this video by Chris Hay, which gets credit for the code and the explanation below.

// hello world

.global _start
.align 2

// main
_start:
    b _printf
    b _terminate

_printf:
    mov X0, #1      // stdout
    adr X1, helloworld      // address of hello world string
    mov X2, #12     // length of hello world
    mov X16, #4      // write to stdout
    svc 0           // syscall

_terminate:
    mov X0, #0      // return 0
    mov X16, #1     // terminate
    svc 0           // syscall

// Hello world string
helloworld: .ascii "hello world\n"

Ok, so what is going on here? Now we're giving that computer direct, low-level commands to the processor. Let's focus on what's going on underneath my comment "//main." Without going into a larger discussion around computer architecture, we'll summarize the procedure. You are in no way supposed to fully get what's going on here. You're just supposed to understand that there's a lot that happens under the hood. With that in mind, read on.

We first have to prepare the computer to output "hello world." In the _printf function, we're going to set the output stream (stdout) in the register (CPU memory slot) X0. Then we're going to create a memory address for our string, which we're naming "helloworld" and store the address (not the string, just the place in memory that will hold the string) in register X1. Then we're going to tell the computer the length of our string of interest (count the number of characters, including whitespace, plus the newline character), which is 12 characters, which is 12 bytes, and store that in register X2. In X16, we're going to place the instruction to write to stdout. Then we call svc 0, which actually requests the operating system to execute _printf.

Then, we have to tell the computer to terminate the program, which is the _terminate function that we define. The equivalent of return 0 from C is moving the NULL command into register X0. This means that the program executed successfully. Then we move the exit command into X16, where we previously were holding the "write to stdout" command. Then we call svc 0 again, which requests the operating system execuite _terminate after displaying "hello world."

Then, like C, there's a song and dance that converts this instruction set into binary machine code that the computer can read, and then it can actually output "hello world." And then we're done.

So I'm going to cut and paste the python code from above to remind you the sheer volume of things that are swept under the rug:

print("hello world")

These are the levels abstraction. We started with a discussion of these levels of abstraction from psychology to physics. Then we moved to the equivalent in computer science. What you learn in computer science in real time is that understanding what's going on at least one level above and below what you're doing makes you a much better programmer.

What do I mean by that? If I run into a bug in python or R, the issue could very well be a lower level issue, the same way that treating disease has you working with chemistry (eg. small molecule drug development) to treat a problem in biology. In other words, solving hard problems involves seamlessly moving up and down levels of abstraction in, whatever your domain is. So you better be well-versed in the levels of abstraction above and below what you're doing.

Given our discussion on levels of abstraction, quite a lot of so-called hacking (both security hacking and innovation) works by means of understanding things one or more levels underneath what you're doing. A much larger discussion of this can be found from this amazing article written by Gwern that I've read many times (and have since written about). But let me paste the punchline, as food for thought:

In each case, the fundamental principle is that the hacker asks: “here I have a system W, which pretends to be made out of a few Xs; however, it is really made out of many Y, which form an entirely different system, Z; I will now proceed to ignore the X and understand how Z works, so I may use the Y to thereby change W however I like”.

In other words, the hacker looks at a thing, and realizes that the thing is merely an abstraction made out of atoms or bits or whatever other low-level object, and it's just a matter of moving those bits/atoms around in a particular way, and they get what they want. I'll paste another bit from Gwern's article to really solidify this.

In hacking, a computer pretends to be made out of things like ‘buffers’ and ‘lists’ and ‘objects’ with rich meaningful semantics, but really, it’s just made out of bits which mean nothing and only accidentally can be interpreted as things like ‘web browsers’ or ‘passwords’, and if you move some bits around and rewrite these other bits in a particular order and read one string of bits in a different way, now you have bypassed the password.

There is one more insight here that I have to continually remind myself over and over: in a competitive activity, you have to both be excellent at the thing (aka do the work) and know the hacks. This can be exemplified with speedrunning, which is a hobby in video gaming where you try to beat a game as fast as possible. Here, you can't just do a hack and call it a day (everyone is looking for the "hack" these days). From Gwern:

In speed running (particularly TASes), a video game pretends to be made out of things like ‘walls’ and ‘speed limits’ and ‘levels which must be completed in a particular order’, but it’s really again just made out of bits and memory locations, and messing with them in particular ways, such as deliberately overloading the RAM to cause memory allocation errors, can give you infinite ‘velocity’ or shift you into alternate coordinate systems in the true physics, allowing enormous movements in the supposed map, giving shortcuts to the ‘end’ of the game.

To get a feel for this, have a look at this history of Mario Wonder speedrunning (which includes info about speed runs in other video games). Someone learns some exploit that the game designers did not anticipate, then everyone is doing that exploit with maximal skill with the character, and then someone learns a new exploit, and the cycle continues. So you have to know both the hacks (be able to operate at lower levels) and have maximum talent (be able to operate at higher levels). Put differently, a biologist needs to know chemistry, but also needs to be a really good biologist.

Taken together, in terms of being a better thinker, it's good to know how things work at least one level under whatever you're doing. I'm not the first to say this by any means. Are you a biologist, at least be familiar with if not competent in chemistry. Are you a python programmer, at least be familiar with if not competent in C. Broadly learn how things work (which is really just another way of saying to look at a thing at a level of abstraction below wherever you're at).

Coding really solidifies this concept and teaches you what it feels like to think at a high level (program in python) versus to think at a low level (program in C or Assembly), and the value of both. Again, I primarily use R and python, but being familiar with the lower level languages too, and the thinking habits they have taught me, has paid off many times over.

Computer science gives us data structures and algorithms that don't come easy to standard spoken language. One of these concepts is recursion. In recursion, you're defining a function where the function is executed in the function definition. Ok, that's a mouthful. Let's try again. What is recursion?

def factorial(x):
  if x < 2:
    return 1
  else:
    return x * factorial(x - 1)

Still a bit mind-bending if you've never seen this before. If this is new to you, get out some paper and draw out the procedure for factorial(5), treating the above as a recipe. Try drawing it out before you look at my sketch below. Ok, now here is my sketch:

Want another example? Just do a Google search on recursion, and they give you the following joke:

But where does this mind bending concept show up in the world? All over the place. One example we have all seen is the concept of fractals. A lot of fractals involve making a shape, like a line that bifurcates (forms two branches). And then a rule that says at the tip of each branch, bifurcate again. And at the tip of those branches, bifurcate again. So you get something like this image, from the Wikipedia article on "fractal canopy" (image by Claudio Rocchini, licensed under CC BY-SA 3.0):

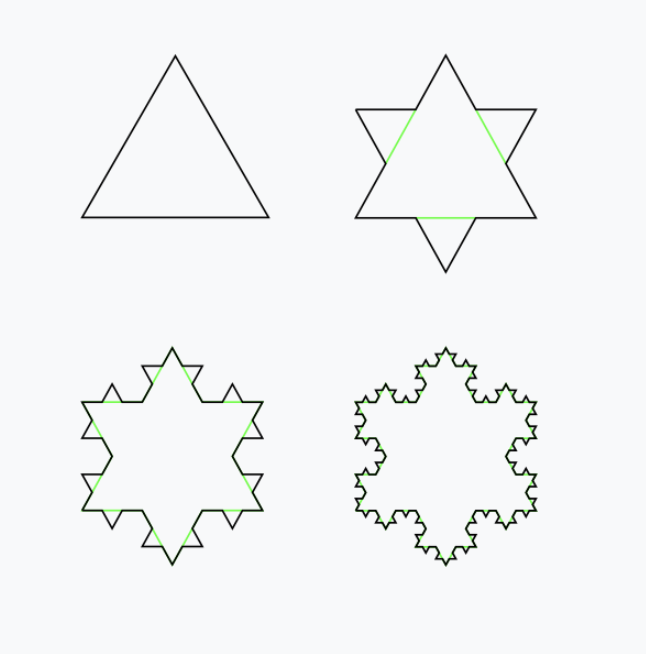
And where do we see this in the real world? How about snowflakes? One way a snowflake can be modeled is by starting with an equilateral triangle, and then at the center of each line, creating a smaller equilateral triangle. And then at the center of these lines, creating a smaller equilateral triangle. This is called a Koch snowflake, and from an image from the linked Wikpedia article on it, you can get a feel for how this works (image by Wxs, licensed under CC BY-SA 3.0):

In biology, there are examples of recursion that show up in the strangest places, like romanesco broccoli. I saw this for the first time at my college dorm cafeteria my sophomore year, before I knew anything about recursion, and I was transfixed because I knew there was something special going on here that I couldn't quite put into words. Now the concept of recursion allows me to put it into words, just as so much of computational thinking has given words to things I couldn't otherwise make explicit. From the linked Wikipedia article above, here is what I saw in Stanford's Wilbur Hall cafeteria (image by Ivar Leidus, licensed under CC BY-SA 4.0):

You can see a pattern, in which at each point, a smaller instance of the same pattern is being constructed. The pattern is being defined within the pattern. Just like in the factorial code example from earlier, where the function is being defined within the function.

There's a fantastic book called Gödel, Escher, Bach by Douglas Hofstadter. A key theme in the book is recursion [1]: these functions that talk about themselves. He uses this self reference to explain Gödel's Incompleteness Theorems. This is a rabbit hole worth another article or several, but in a nutshell, he shows that formal systems (eg. math, language) start to break down if you get them to talk about themselves.

Want an example? Evaluate the truth of:

The following sentence is true.
The preceeding sentence is false.

If the second sentence is true, then the first sentence is false, but the first sentence says that the second sentence is true, which would in turn make the second sentence false, but if the second sentence is false then the first sentence is true. Um…what? Anyway, this is a small but important sliver of the context around Gödel's Incompleteness Theorems, one of the most important contributions to mathematics in human history.

If all of this seems a bit mind bending, it is because it is. I first came across this when I attempted to read Gödel, Escher, Bach for the first time when I was a teenager. Most of it went over my head, but this sentence pair above stuck around in my head for decades.

It wasn't until I read the book after I had taken my computer science courses and was coding daily for work that I could finally wrap my head and these things. The concept of self reference in formal systems, and the concept of recursion is hard to grasp, but it runs very deep, shows up across many domains of study, and it is absolutely worth learning. How do you learn it? By a combination of looking at examples, and importantly, learning how to code and solving problems that require you to write recursive programs.

If you don't get this stuff right away, don't worry about it. Look at the images in this section, and let them sink in for a few days or months. Even when I was actvely learning and focusing on recursion (in my second computer science class, CS106B), it still took me a month or two before the concept really sunk in. And that's ok.

Ok, how about a practical example for biologists. What is a cell signaling pathway? Well, to massively oversimply, you have messages being passed from protein to protein all the way down to the DNA where some sort of effector (eg. a transcription factor) does a thing to the DNA. What if you wanted to model that? How would you do it? Well, in computer science (and discrete math) there is a data structure called a graph that allows for one to wire up a pathway in silico. This is a graph as in a mathematical abstraction of a network, not to be confused with a biaxial plot.

Here's what the graph representation of a piece of a pathway looks like in base python, using a dictionary (again, confusing wording…it's a look-up table):

graph = {
   'RAS':'RAF',
   'RAF':'MEK',
   'MEK':'MAPK',
   'MAPK':['MNK', 'RSK', 'MYC']
}

So now let's wire one up. Ok, done. What do I get from that? Well, one very fundamental question in graph theory is what are the "central" regions of a graph? This is called centrality. Degree centrality tells us how many friends each node has. Betweenness centrality tells us what regions in the network have the most shortest paths that run through them.

Think of the Bay Bridge from Oakland to San Franscisco. Commuters know that, minus traffic, that is the quickest path to San Francisco for a lot of the East Bay and beyond. The Bay Bridge would have a high betweenness centrality. But with this metric you can quantify that and compare it to the San Mateo bridge to the south.

Such is the same with signaling pathways. Assuming you have a good dataset, you can start interrogating these pathways in terms of regions that are relevant to whatever your intent is. How do I know this? I spent three years doing just this for a client of mine. The use case is simple (though the implementation is complicated): can we find druggable regions of the network that will lead to the change that we want given the intent of the company? It would have been very hard, if not impossible, to do this kind of work without the intuition and use of a graph.

When you start thinking in terms of graphs and using graphs as part of your problem solving toolkit, difficult "systems level" problems in biology, like those around signaling pathways, start to become more actionable.

As an example of complicated signaling pathways, anyone who studies biochemistry ultimately comes to the realization that we can't wrap our heads around every little intricate detail of cellular metabolism, aside from perhaps the memorization of the high-level pathways like the Citric Acid Cycle which everyone does in their intro bio classes. But the reality of cellular metabolism looks more this like image below, taken from the Wikipedia article on metabolic pathways (image by Chakazul):

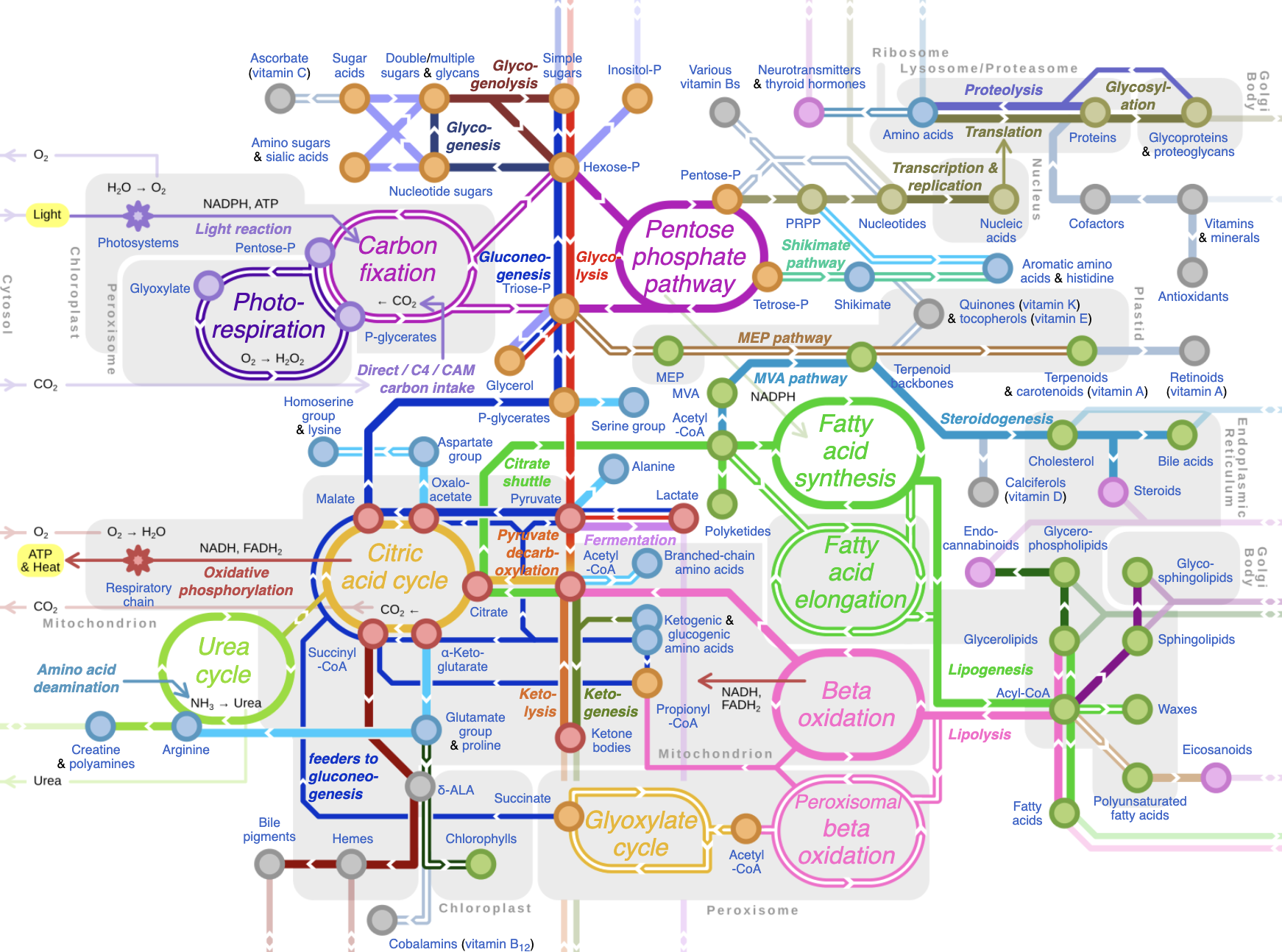
Note that this is a map not of the pathway, but a map where the nodes are metabolites and the edges are individual pathways. In other words, to look at what each metabolite gets converted to in each pathway, this map gets much, much more complicated. So then when you get to this level and you want to understand what nodes and connections are more inflential, and what happens in theory when something is perturbed, it becomes a problem for computers. And if you are well versed in computational thinking, then this becomes a doable task [2].